木屑压缩成型颗粒圆周表面形貌分形参数研究

德雪红¹，张博文¹，金敏¹，吴桂芳¹，翟晓敏²，郭文斌¹

（1.内蒙古农业大学机电工程学院，呼和浩特010020；2.航天科工集团第六研究所，呼和浩特010076）

　　摘要：精确地表达生物质成型颗粒圆周表面粗糙形貌是生物质成型机关键部件摩擦磨损机理分析及磨损预测研究的关键。选择原料为混合木屑的生物质成型颗粒，在直径6mm、颗粒度1~3mm、含水率11%、密度1.2g/cm³的条件下，测出其圆周表面形貌及轮廓数据，利用成型颗粒圆周表面粗糙形貌所具有的统计自相似性和标度不变特性，采用盒子计数法、结构函数法、变差法3种方法分别计算出成型颗粒圆周表面的分形维数D和分形特征参数G，再根据W-M分形函数，建立生物质成型颗粒圆周表面粗糙形貌的分形函数模型，进行了数值模拟。结果表明：木屑压缩成型颗粒圆周表面粗糙度均值为1.45μm时，D的均值约为1.6，G值约为2.24×10^-5m。分形模型对木屑压缩成型颗粒圆周表面的粗糙形貌模拟准确合理，所测得的分形参数准确；在测定分形维数D的过程中，盒子计数法的计算精度相对更高。本研究为重构准确可信的生物质成型颗粒圆周表面粗糙形貌数字化模型，实现成型颗粒圆周表面与成型模具接触状态仿真分析奠定基础。

　　生物质成型颗粒圆周表面粗糙形貌是精确分析生物质成型颗粒表面与成型模具之间相互接触作用的基础，是分析成型模具所受摩擦磨损机理并实现其磨损预测的关键。而重构准确、可信的生物质成型颗粒圆周表面粗糙形貌数字化模型，是成型颗粒圆周表面与成型模具接触模拟仿真，以及成型模具力学性能、摩擦磨损机理分析及磨损预测的关键[1-2]。

　　分形理论自20世纪由Mandelbrot创建以来，已广泛应用于分析和处理具有复杂细节特征的自然现象[3-6]。分形理论对描述具有标度率特点的自然现象具有较好适用性[7-10]，此外，生物质成型颗粒圆周表面粗糙形貌也具有统计自相似性和标度不变特性[11-14]，因此，可利用分形理论对生物质成型颗粒圆周表面粗糙形貌进行分析。

　　近年来，一些学者[15-20]先后开展了利用分形理论研究金属接触表面间的真实接触状况，以解决金属与金属接触面间的摩擦机理问题，进而预测摩擦磨损状况，但目前还鲜见利用分形理论对生物质成型颗粒外表面做的相关研究，以及对其与成型孔内壁真实接触状况进行理论分析。笔者用盒子计数法、变差法、结构函数法3种算法分别计算出成型颗粒圆周表面分形参数D和G，并以此为基础，利用W⁃M分形函数，建立起生物质成型颗粒圆周表面粗糙形貌分形模型，再通过数值模拟，实现其表面形貌重构，力求利用W⁃M分形函数构造出更具普遍意义的生物质成型颗粒圆周表面粗糙度曲线。

　　1理论分析及模型建立

　　因环模成型模孔粗糙表面具有分形特征，基于表面分型参数接触模型能够客观反映粗糙表面的接触性质，故所建摩擦力公式具有科学性[11-15]。经典接触力学指出，当固体表面既承受法向载荷又承受切向载荷时:若两力比值小于0.3，屈服将发生在表层以下；若两力比值大于0.3，屈服将发生在接触点的边缘[15-18]。摩擦分子机械理论指出，在外力作用下，两摩擦表面间的作用可分为机械作用和分子作用两种，即指由于弹塑性变形、微凸体间相互碰撞、啮合及犁沟效应等而阻碍的相对滑动，以及由于分子力作用和分子活动使接触微凸体发生黏附而产生的滑动阻力[17]。表面间分子作用力与机械阻力之和的切向分量即为摩擦力。

　　2表面轮廓分形维数计算方法

　　分形理论作为现代数学的一个分支，可以从分数维度的视角来描述和研究具有自相似性的、不规则的几何图形（如山脉、树木等）问题[17]。针对生物质成型颗粒圆周表面粗糙形貌的研究，选取计算分形维数常用的3种方法———盒子计数法、变差法、结构函数法分别进行分形维数的测定。

　　3参数测定及试验分析

　　3.1试验条件

　　试验用成型颗粒样本由木屑（呼和浩特市周边的松树和杨树混合木屑）经生物质成型机压缩制成，其颗粒度为1~3mm、含水率约11%、密度约1.2g/cm³。样本制作工艺流程:生物质环模成型机由电机（功率7.5kW）带动环模旋转，物料与环模间摩擦力和物料与压辊间摩擦力使压辊自转，物料在环模与压辊间形成的楔形空间受挤压力作用而被挤入环模成型孔（成型模孔长径比5∶1）内，并逐渐从环模孔以柱状形式被挤出。

　　主要测试仪器:JB⁃8C型精密粗糙度仪（广精精密仪器有限公司）；DHS⁃10A型快速水分测定仪；100mL量筒（精度1mL）；网孔直径3mm的标准检验筛（符合GB/T6003.1—1997《金属丝编织网试验筛》要求）；JAEIHAENE型电子秤（精度0.01g）；游标卡尺；秒表（精度0.01s）。

　　3.2试验方法

　　将生物质环模成型机生产的直径为6mm的木屑压缩成型颗粒，进行密度和含水率的测量，然后利用粗糙度仪对成型颗粒圆周表面粗糙形貌进行测量并提取数据，再利用3种分形维数方法计算成型颗粒圆周表面粗糙形貌的分形维数D。

　　3.2.1成型颗粒密度计算

　　取若干成型颗粒，将其端面磨平后采用游标卡尺测出颗粒长度与直径，并称得质量，最后求得颗粒密度。

　　3.2.2表面粗糙形貌测量

　　选出直径为6mm的10组（每组10个成型颗粒样本）木屑压缩成型颗粒样本，利用粗糙度仪对每一颗粒样本的圆周表面粗糙状态进行轴向形貌测量，获得表面轮廓曲线，提取其表面轮廓曲线数据后，再利用3种分维算法计算生物质成型颗粒圆周表面粗糙形貌分形维数D值。

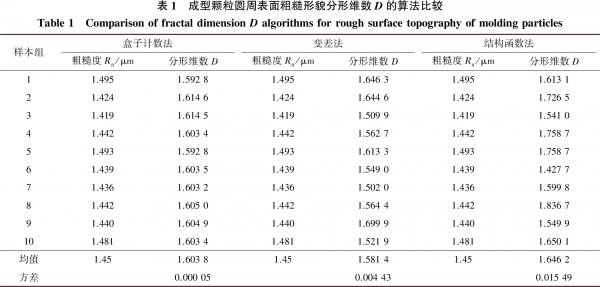
　　1）盒子计数法。根据盒子计数法计算分维的原理，实现不同大小的网格（设n=1，2，…，11）对所测样本粗糙表面轮廓进行动态覆盖，再利用MATLAB对网格边长2-n和网格数目2n分别进行统计，再采用最小二乘法对二者进行对数拟合，所拟合出的图形斜率α（图3）绝对值即为分形维数D值，计算结果如表1所示。

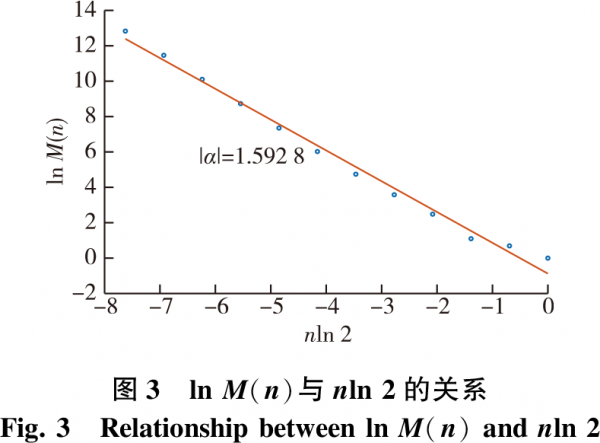
　　2）变差法。对所测样本粗糙表面轮廓形貌，分别取尺度r为1，2，…，10μm，测出对应的Hi值，利用式（8）计算出对应的V（r）值，建立lgV（r）与lgr为坐标轴的散点图，进行数据拟合后得出直线，求出斜率α（图4），将其绝对值代入式（9），求得分形维数D值，计算结果如表1所示。

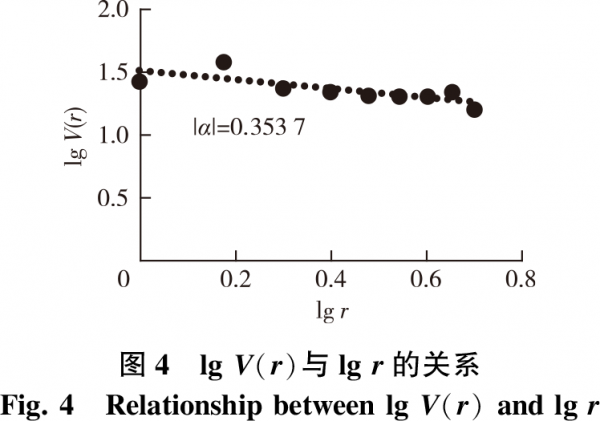
　　3）结构函数法。对所测样本粗糙表面轮廓形貌，分别取θ为1，2，…，10μm，测出对应的表面粗糙高度z（x+θ）及z（x）值，并利用式（10）计算出对应的S（θ）值，建立lgS与lgθ为坐标轴的散点图，进行数据拟合后得出直线，求出斜率α（图5），将其绝对值代入式（11），求得分形维数D值，计算结果如表1所示。

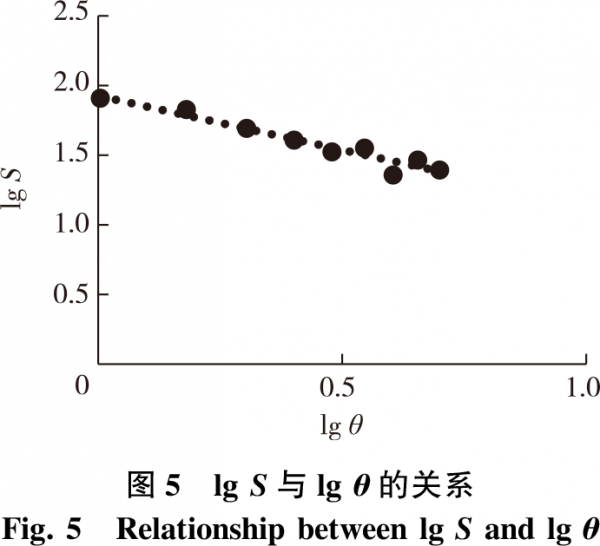
　　3.3试验结果与分析

　　所取样本经过3种分维算法后得到的生物质成型颗粒圆周表面粗糙形貌分形维数D值见表1。由表1可知，生物质成型颗粒圆周表面的粗糙度均值为1.45μm时，粗糙形貌分形维数D的均值约为1.6（保留一位小数后）。样本表面轮廓采样长度L取50μm，其轮廓的分辨率δ取0.001，并与分形维数D一起代入式（6）后计算得出分形特征参数G=2.24×10^-5m。

　　由表1分析可知，盒子计数法、变差法及结构函数法3种算法所测出的分形维数D相同，均约为1.6，但略有区别。结构函数算法计算D所得数据最大，D的均值达到1.6462，方差也最高，达到0.01549；变差算法计算D所得数据最小，D的均值为1.5814，方差达0.00443；盒子计数法计算D所得数据居中，D的均值为1.6038，方差最小，仅为0.00005。因此，经分析得出，由于盒子计数法计算所得样本方差相对最小，用环模生物质成型机生产的密度为1.2g/cm³的生物质成型颗粒圆周表面粗糙形貌的分形维数D测量中，采用盒子计数法计算分形维数D值相对精度更高。

　　4成型颗粒表面粗糙形貌模拟

　　4.1二维仿真模拟

　　将上述计算结果代入式（6）后，编写二维随机粗糙表面程序，利用MATLAB进行模拟计算，对成型颗粒圆周表面粗糙形貌进行数值模拟。具体参数设置:分形维数D=1.6，分形特征参数G=2.24×10-5m，轮廓分辨率δ=0.001，轮廓采样长度L=50μm。模拟后的结果如图6所示。

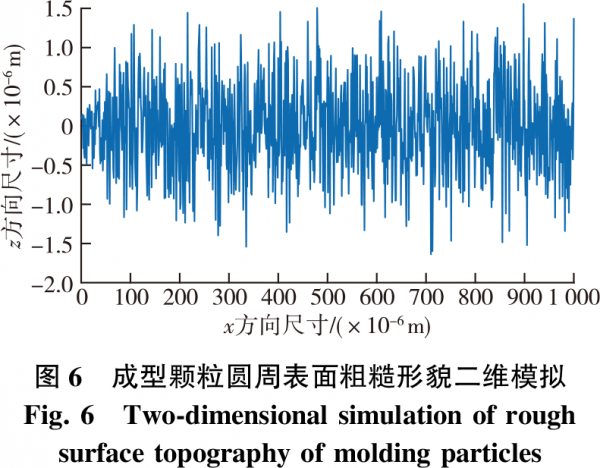
　　4.2三维仿真模拟

　　根据上述计算结果，对成型颗粒粗糙表面轮廓，利用式（6）在MATLAB中进行计算后再经过三维空间随机转化计算，得到的三维形貌视图结果如图7所示。

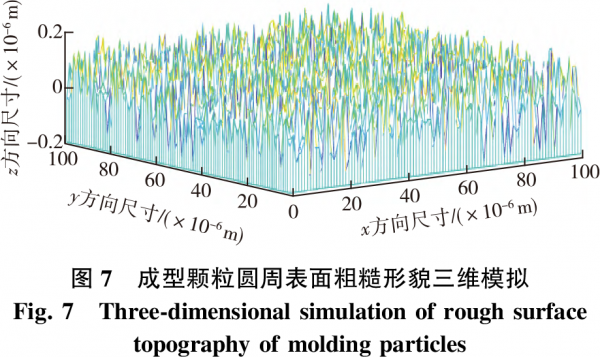
　　4.3模拟试验结果分析

　　将实测木屑成型颗粒粗糙表面所得分形参数D、G作为数据仿真的初始值，利用W⁃M分形函数对其轮廓形貌进行模拟，结果如图6（二维视图）和图7（利用MATLAB进行随机转化得到三维视图）所示。成型颗粒圆周表面粗糙形貌电镜放大100倍下的扫描状态见图8，其中暗色区表示颗粒表面比较光滑，白色线条区表示非光滑表面，白色线条越多表明成型颗粒圆周表面孔隙越多、密度越低，也越粗糙。

　　为了对模拟结果进行分析，需要对图3中的模拟粗糙形貌数据进行采集后与图8的表面粗糙形貌作对比分析。针对木屑压缩成型颗粒表面粗糙形貌的轮廓算数平均偏差Ra、平均轮廓波峰高度Rp、轮廓单元平均宽度Rsm、粗糙度峰值数Rpc、轮廓支承比率Rmr这5个重要参数进行对比探讨。图3中，模拟轮廓算数平均偏差Ra=1.432μm（实测Ra=1.495μm），模拟平均轮廓波峰高度Rp=2.84μm（实测Rp=2.776μm），模拟轮廓单元平均宽度Rsm=0.178mm（实测Rsm=0.182mm，如图8所示），模拟粗糙度峰值数Rpc=30峰/mm（实测Rpc=32.5峰/mm），模拟轮廓支承比率Rmr=89.8%（实测Rmr=93.6%）。

　　根据上述数据分析结果，模拟参数Ra、Rp、Rsm、Rpc、Rmr与实测参数接近程度（模拟值/实测值）分别为95.8%，102.3%，97.8%，92.3%，95.9%，说明利用W⁃M分形函数模拟木屑压缩成型颗粒数据基本准确合理。由此可知，所测得的分形维数D及分形特征参数G正确，所用粗糙表面分形模拟模型对生物质成型颗粒圆周表面粗糙形貌的模拟是合理的。

　　5结论

　　对于以混合木屑为原料、颗粒度1~3mm、含水率11%、直径6mm、密度1.2g/cm³的生物质成型颗粒，采集其圆周表面粗糙形貌数据，采用盒子计数法、结构函数法、变差法3种方法分别计算出粗糙表面分形模型的关键参数（分形维数D和分形特征参数G），再根据W⁃M分形函数，建立了生物质成型颗粒圆周表面粗糙形貌分形模型，并进行数值模拟，得到如下主要结论。

　　1）生物质成型颗粒圆周表面的粗糙度均值为1.45μm时，粗糙形貌分形维数D的均值约为1.6，分形特征参数G约为2.24×10^-5m。

　　2）模拟结果表明，粗糙表面分形模拟模型对生物质成型颗粒圆周表面的粗糙形貌模拟准确合理，所测得的分形维数D及分形特征参数G准确，所用粗糙表面分形模型对生物质成型颗粒圆周表面粗糙形貌的模拟是合理的，且具有普遍意义。

　　3）采用盒子计数法、变差法及结构函数法3种方法测定生物质成型颗粒圆周表面粗糙形貌分形维数D的过程中，盒子计数法的计算结果最可信，计算精度相对更高。